■トップページ
■算数・数学スーパー個別指導のご案内
■灘中学算数入試問題
■おもしろ算数問題 50問(中学入試)
■中学受験算数を楽しく極めたい(ブログ)
■算数イベントなどの写真
■最近行った所
■お問い合わせ
この下に続くおもしろ算数問題の中から
あなたのお気に入りの問題がひとつでも見つかるといいですね
自分の頭で考える喜びを味わってみてください
解けた瞬間の感動の喜びをあなたも味わってみて〜〜それでは、ごゆっくりどうぞ
毎年、たくさんの良問を出題してくれる灘中の先生に感謝します。ありがとうございます。
灘中学 入試問題 2022年度 ( 令和4年度 )入試 算数1日目 4番 整数 余り 合同式 2の累乗(べき乗) 2を10個かけてできる数 2×2×2×2×2×2×2×2×2×2を 17で割った余りは □ です。 また、2を2022個かけてできる数 2×・・・・・・・・・×2を 17で割った余りは □ です。 解き方 前半 1×2×2=4 後半 17ー2×2=13 答えはすぐに出せると思いますが、 答えにいたる途中過程を工夫すると あなただけのオリジナルな計算方法が発見されることもあり ほかの問題にもその同じ計算方法が使えて どんどん楽しくなりますよ 答え 順に 4 13 |
灘中学 入試問題 2022年度 ( 令和4年度 )入試 算数1日目 5番 整数 場合の数 偶奇性 式の扱い 分配法則 余事象 A、B、C、Dは1以上10以下の整数です。 A、B、C、Dの中に同じ整数が含まれていてもよいものとします。 A×B+A×C+A×D+B×C×Dが偶数となるような A、B、C、Dの組は全部で □ 組あります。 解き方 A、B、C、D の偶数、奇数で場合分けする 104 ― (5×53+5×53×3)=7500 答えはすぐに出せると思いますが、 答えにいたる途中過程を工夫すると あなただけのオリジナルな計算方法が発見されることもあり ほかの問題にもその同じ計算方法が使えて どんどん楽しくなりますよ 答え 7500 |
灘中学 入試問題 2022年度 ( 令和4年度 )入試 算数1日目 1番 計算 逆算 通分 方程式 分数 素因数分解 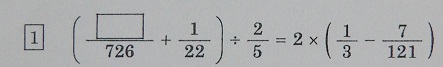 解き方 726=121×6 726=22×33 726=3×242 (□+33)×5=4×(242―42) □=4×200÷5−33=127 127は素数です 答え 127 |
灘中学 入試問題 2022年度 ( 令和4年度 )入試 算数1日目 3番 食塩水 濃度 てんびん算 逆比 濃度が □ %の食塩水が □ g 入っている容器に、 濃度が1.9%の食塩水100gを加えてよくかき混ぜると、 濃度が3.1%になりました。 そのあとに食塩10gを加えてよくかき混ぜると、 濃度が5%になりました。 解き方 てんびん図をかく (100−5)×10÷(5−3.1)=500 500−100=400 3.1+(3.1−1.9)÷4=3.4 答え 順に 3.4 400 |
灘中学 入試問題 2022年度 ( 令和4年度 )入試 算数1日目 2番 式の扱い 方程式 整数 仕事算 比 逆比 ある仕事に兄と弟が取り組みます。 兄は30分働くごとに5分休むことを繰り返します。 弟は働き始めると休まずに働き続けます。 兄が働き始め、その95分後に弟も一緒に働き始めると、 兄が働き始めてから135分後にこの仕事が終わります。 また、弟が働き始め、その90分後に兄も一緒に働き始めると、 弟が働き始めてから、140分後にこの仕事が終わります。 この仕事を弟だけで終わらせるには □ 分かかります。 解き方 [ 30 ]×4+<40>=<140>+[ 30 ]+[ 15 ] [ 75 ]=<100> [ 3 ]=<4> [ 120 ]+<40>=<160>+<40>=<200> 答え 200 |
2022年度 灘高校 数学 4番 確率 場合の数 場合分け A,P,Sの3種類の文字から無作為に1文字を選ぶことを繰り返し行い、 選んだ文字を選んだ順番に左から右に向かって1列に並べていく。 (1) 文字を6個並べたとき、 「PASS」という連続した文字の並びが含まれる確率を求めよ。 (2) 文字を9個並べたとき、 「PASS」という連続した文字の並びが含まれる確率を求めよ。 解き方 (1) PASS○○ ○PASS○ ○○PASS の3パターン (32×3)/ 36=1/27 (2) ア PASS○○○○○ イ ○PASS○○○○ ウ ○○PASS○○○ エ ○○○PASS○○ オ ○○○○PASS○ カ ○○○○○PASS PASSPASS○ がアとオ PASS○PASS がアとカ ○PASSPASS がイとカ で2回数えられていることに気をつけて (35×6―3×3)/ 39=161/2187 答えはすぐに出せると思いますが、 答えにいたる途中過程を工夫すると あなただけのオリジナルな計算方法が発見されることもあり ほかの問題にもその同じ計算方法が使えて どんどん楽しくなりますよ 答 (1) 1/27 (2) 161/2187 |
灘中学 入試問題 2019年度 ( 平成31年度 )入試 算数1日目 6番 倍数 大きな素数 試行錯誤 実験 89の倍数と113の倍数を、 89,113,178,226,・・・・・・・・ のように小さいものから順に並べるとき、 50番目の数は □ です。 解き方1 大ざっぱ法でいきます ほとんど計算しないで答えが出せる気持ちよさ、感覚が、 あなたにも伝わればうれしいです 89も113も素数であることに注意する 89と113の比は88:112=11:14に近いと考えます ここで11+14=25であることに気づくとラッキーです 問題文の50番目の50は25の2倍ですから、 88×28と112×22の掛け算の結果2464は出さなくても 88の倍数の28番目と112の倍数の22番目は同じです 88×28=112×22です 89×28は88×28より28大きい 113×22は112×22より22大きい ことに気をつければ、 89×28が小さい方から50番目だと分かります 線分図を書いてあげると理解しやすいかもです 89×28=(90−1)×28=2520−28=2492 解き方 2 50個を25個ずつに分けてみてから、調整する 89の倍数の25番目と113の倍数の25番目の差は 24×25=600です 600の差を意識して 89の倍数を3個増やし113の倍数を3個減らすと (89+113)×3=606 よって89×28が50番目と分かる 89×28=(90−1)×28=2520−28=2492 解き方 3 小さい順に7個で差が17に気づく 89×4=356 113×3=339 差が17なので、これを7セット 89×28は113×21より119大きいので 113を1個追加すると 89×28は113×22より6大きいことになる よって、89×28=2492 解き方 4 小さい順に9個で差が7に気づく 89の倍数 89 178 267 356 445・・・・・・ 113の倍数 113 226 339 452・・・・・・ 89 113 178 226 267 339 356 445 452 小さい順に並べると89の倍数と113の倍数が交互に出てきますが、 7番目と8番目が連続して89の倍数が出てくる 8番目と9番目の差が24×4−89=7 89×5=445 113×4=452 差が7で、これを5セット 113×20は89×25より35大きい 35大きいことを意識して、残り5個を 89の倍数3個、113の倍数2個追加すると 50番目は89の倍数の28個目で 113の倍数の22個目より6大きくなる よって、89×28=2492 楽しんでいただけましたでしょうか 答え 2492 |
灘中学 入試問題 2021年度 ( 令和3年度 )入試 算数1日目 3番 整数 場合の数 2021の各位の数の和は2+0+2+1=5 です。 このように、各位の数の和が5である4桁の整数は、 2021を含めて全部で □ 個あります。 そしてそれらの整数の中で2021は小さい方から数えて □ 番目です。 解き方 前半 組合せの公式を使う 解き方1 7C3=35 解き方2 8C3―7C2=56―21=35 解き方3 6C2+5C2+4C2+3C2+2C2 =15+10+6+3+1=35 後半 6C2+3=18 答え 順に 35 18 |
灘中学 入試問題 2021年度 ( 令和3年度 )入試 算数1日目 5番 整数 平方数を15で割った余り 合同式 Aは2桁の整数で、A×Aを15で割ると1余ります。 このようなAは全部で □ 個あります。 解き方 100=15×6+10 (4×6−2)+2=24 答え 24 |
灘中学 入試問題 2021年度 ( 令和3年度 )入試 算数1日目 7番 整数 場合の数 7の倍数 Xは3桁の整数で、どの2つの位の数も異なります。 Xを7倍すると4桁の整数ABCDを作ることができ、 A>B、 B>C、 C>D、 D>0となりました。 このとき、Xは □ です。 解き方 4321以上6543以下で調べる 4321以上5000未満 1個 5000以上6000未満 4個 6000以上6543以下 10個 を調べます 答え 903 |
おもしろ算数問題 2022年(中学入試)にチャレンジはコチラ →おもしろ算数問題 2022年(中学入試)
灘中学 入試問題 2016年度 ( 平成28年度 )入試 算数1日目 5番 オイラーの関数 素数 互いに素 1000以下の整数のうち、2でも3でも5でも割り切れない整数を 小さいものから順に並べると 1,7,11,13,17,・・・・・・・,997 となります。 このなかで、一の位の数が7である整数は全部で□個あります。 また、7で割り切れる整数は全部で□個あります。 解き方 素数の楽しさを味わえる問題です 問題文の中に10以下の素数2,3,5,7が全て出てきています 2,3,5の最小公倍数は30ですから、1から30までの整数のなかで 2でも3でも5でも割り切れない整数を 書き出していきます でもここで、問題文のなかに 1,7,11,13,17というように17までは書いてくれています ここで灘の算数の問題は分かる人だけに分かるヒントが 問題文の中や例の中に隠されています 別に1,7,11,13,・・・・・・・,997というふうに問題分を書いても、 1,7,11,・・・・・・・,997と書いてもいいと思いませんか? それなのにどうして1,7,11,13,17というように17まで 書いてあるのでしょう? そのあと全部2,3,5で割り切れないことをチェックしていってもいいのですが、 13+17=30が使えることを知っている人だけに ちょっとでも有利になるように17まで書いてくれていると思います。 そこまで算数を楽しんでいる人を 灘が求めているのではないでしょうか? ここで灘中に上位合格する人たちが知っていることを 書いておきます ワンポイントアドバイス 13+17で30ですね あとは30−11で19 30−7で23 30−1で29となります(説明略) だからいっきに 1,7,11,13,17,19,23,29と書き出せます あとは30ごとに繰り返します 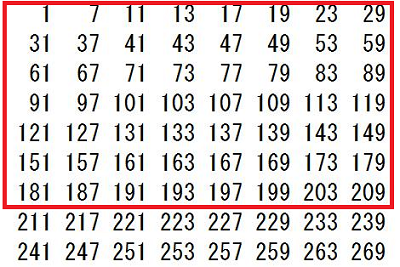 30までに一の位が7であるのは2つあります 1000÷30=33・・・10 2×33+1=67 灘中に上位合格する人たちは上の数表すべて書き出していません 前半の問題を解くのに 実際の試験上で計算用紙に書き出しているのは 最初の一行(1,7,11,13,17,19,23,29)で十分です 30ずつ繰り返すので、書かなくていいことが頭のなかでわかっています 30ずつ繰り返すことを意味も分からず、ただ覚えるのではなく、 理由を考えてみましょう。そうすると、 最初の一行で十分であることが理解できますね 最小公倍数のすごさ、素数のすごさ、繰り返すことのすごさを 感じられるのではないでしょうか つぎに後半の解き方ですが 30と7の最小公倍数は210ですので、 210までのなかで7で割り切れる整数をみつけます 上の表の赤枠の中で7の倍数は何個ありますか? これから受験の方は時間を計ってやってみましょう この作業がわりと時間がかかりますし、 計算ミスの可能性もありますね。 100までの7の倍数は普段練習しているので すぐに判定できると思います 100超えてからの7の倍数判定が時間がかかると思います 赤枠の中の4行目91を見つけてほっとしませんでしたか? これは一行に一つ7の倍数があるからあとは簡単と思ったら落とし穴に はまってしまいます 119も7の倍数ですよ 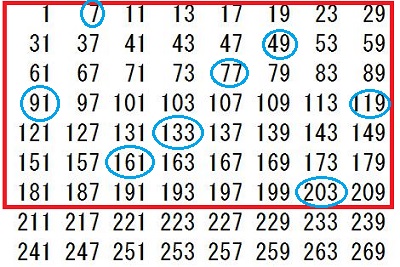 119が7の倍数であることを見つけても 121から209までの24個の整数全部を7で割るのはしんどいですよね? ここで違う思考回路を紹介します 使っている方も多いと思いますが 119が7の倍数とわかったら、そのことを活用するのです 7の倍数に7を足しても7の倍数ですね 頭のなかで126は表にないな 次は133これは表にある 140,147,154・・・・・・・という感じでやる方法です 時間がたっぷりあるときはもちろんどんな方法でもいいです これで赤枠の中に7の倍数が8個あることがわかりました 1000÷210=4・・・160 赤枠の中で160までの7の倍数は6個だから 8×4+6=38 これで答えは出ましたが、何か気づきませんでしたか? 赤枠をよ〜く見てください 今度は縦に数字を見ていってください どの列にも7の倍数が1つずつありますね これは偶然ではないんですよ 理由がわかったらおそらく感動するかも 縦に見ていくということは30ずつ足していってますね 30を足すということは 30÷7=4・・・2 7で割った余りが2ですから 縦に2を加えていくと7で割った余りになります ということは、赤枠の中全部を7で割る必要がなくなります 最初の一行目(1,7,11,13,17,19,23,29)の整数を 7で割って余りを書き、縦に2を加えていく方法で 0になるところが、7の倍数です 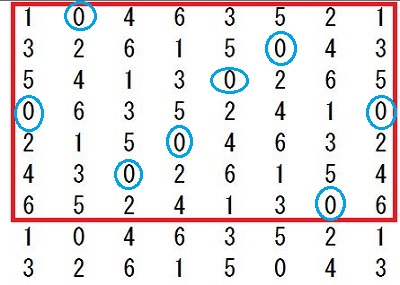 この方法だと大きな数を7で割るという作業をしていませんね だから後半の問題を速く正確に解けますね 問題を解くこととは関係ありませんが 表をよく眺めていると 赤枠の中のど真ん中を点対称の中心として 対応するところを足すと7で割り切れるようになっています 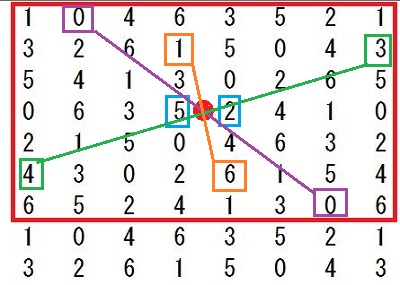 もう一度上の表を見ると、 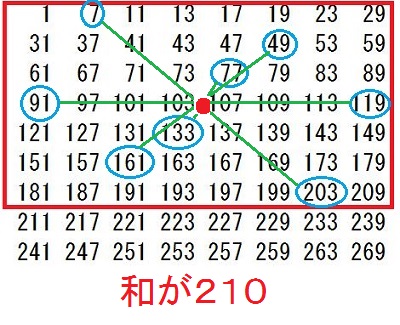 これってすごくないですか? 数の性質って美しいですね ここまで読んでくれたあなたに 最後に後半の問題を表を書き出さずに、 最初の一行(1,7,11,13,17,19,23,29)だけで解く方法を 紹介しておきます この8つの数をそれぞれ7倍してみてください そして、先程の上の表を見てください 先程がんばって探した7の倍数すべて (赤枠の中の青丸で囲んだ数)が 最初の一行(1,7,11,13,17,19,23,29)の7倍に なっていませんか? あまりの美しさに見惚れてしまいます ということは、本当に深く理解していたら、 最小公倍数210までに7の倍数が8個あることと 1000÷210=4・・・160 160÷7=22・・・6 最初の一行をみて、22までだから 1,7,11,13,17,19の6個 8×4+6=38 楽しんでいただけましたでしょうか 答え 順に 67 38 |
算数の受験者平均が1日目も2日目も50%以下だった
2009年灘中学算数入試問題はコチラ → ■2009年灘中学算数入試問題
灘中学 入試問題 2019年度 ( 平成31年度 )入試 算数1日目 4番 合同式 素数 素因数分解 約数 余り A=377×377×377×377×377×377 とするとき、 Aの約数の中で14で割ると1余るものは、 1を含めて全部で □ 個あります。 また、Aの約数の中で15で割ると1余るものは、 1を含めて全部で □ 個あります。 解き方 素因数分解をする 前半 377=13×29 ここで13と29はどちらも素数です A=377×377×377×377×377×377 =13×13×13×13×13×13 ×29×29×29×29×29×29 =136×296 13×13は14で割ると1余る 29は14で割ると1余ることを使って 4×7=28 後半 13×13×13×13は15で割ると1余る 29×29は15で割ると1余る 2×4=8 答え 順に 28 8 |
灘高校入試問題 2009年(平成21年) 数学3番 場合の数 整数 平均 3の倍数 ↑↑↑灘中受験予定の小学4,5,6年生は(3)までやって自信をつけよう〜〜 |
灘中学 入試問題 2019年度 ( 平成31年度 )入試 算数1日目 3番 足し算 虫食い算 場合の数 A,B,C,D,E,F,G,Hはどの2つも異なる2から9までの数字です。 3桁の整数ABCとDEFを足すと4桁の整数10GHになり、 この足し算でくり上がりは百の位から千の位にだけあるとき、 GとHの和は □ です。さらにこのとき、AがDより大きいとすると、 ABCとして考えられる3桁の整数は全部で □ 個あります。 答え 順に 17 16 |
灘中学 入試問題 2019年度 ( 平成31年度 )入試 算数1日目 5番 損益売買算 ある品物を仕入れ、利益を見込んで1個400円で売りました。 しかし、いくつか売れ残ったため、 売値を半額の200円にして残りをすべて売りました。 その結果、売上高は26000円、利益は11600円になりました。 品物1個の仕入れ値は1円未満の端数はありません。 また、400円で売れた品物の個数は 仕入れた品物の個数全体の6割より多く、 7割より少ないことがわかっています。 このとき、品物1個の仕入れ値は □ 円で、 400円で売れた品物の個数は □ 個 です。 答え 順に 180 50 |
2017( 素数 )年中学入試予想問題はコチラ →2017年中学入試予想問題
算数の受験者平均が1日目も2日目も50%以下だった
2009年灘中学算数入試問題はコチラ → ■2009年灘中学算数入試問題
灘中学 入試問題 2016年度 ( 平成28年度 )入試 算数1日目 1番 計算問題 2016の約数 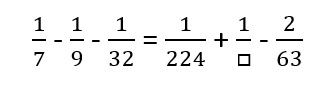 2016の約数は36個ありますよ 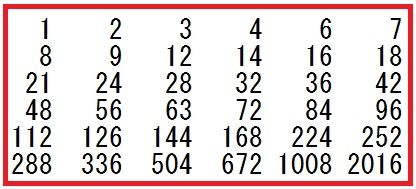 1 2 3 4 6 7 8 9 12 14 16 18 21 24 28 32 36 42 48 56 63 72 84 96 112 126 144 168 224 252 288 336 504 672 1008 2016 分母に出てくる7,9,32,224,63がすべて2016の約数になっています 2016=63×32を覚えていたら安心です 224は覚えていなくても、暗算で9をかけて2016になるかを 慎重にチェックしておきます または暗算で224は7で割ると32になることがわかりますから、 2016の約数であることがわかります 方法1 1/7=288/2016 1/9=224/2016 1/32=63/2016 1/224=9/2016 2/63=64/2016 と分母を2016に合わせてやっていき 1/□=56/2016となり約分して□が36と分かる 方法2 式全体を見て 1/7−1/9=2/63であるから 4/63−1/32−1/224ここで通分する (128−63−9)/2016=1/36 答え 36 |
灘中学 入試問題 2016年度 ( 平成28年度 )入試 算数1日目 2番 水問題 解説のみ 7cmと9cmから 水の量を<63>とする四角柱2本の底面積が<2> 水槽の底面積が<12>となるので、 <63>÷<12>=5.25cm 答え 5.25 |
灘中学 入試問題 2016年度 ( 平成28年度 )入試 算数1日目 3番 カード交換 解説のみ 実際に文章を読んでやってみましょう 算数パズルを解いている楽しい感覚が味わえます 宮本算数教室の賢くなるパズルや 数独のマス目に数字が埋まっていく感覚を思い出しました 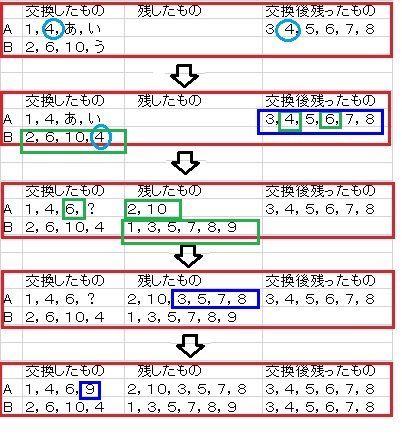 答え あ 6 い 9 う 4 |
灘中学 入試問題 2016年度 ( 平成28年度 )入試 算数1日目 4番 速さ A君とB君が円形のジョギングコースを同じ向きに走りました。 A君とB君は地点Pを同時にスタートし、その9分後に、 A君はちょうど6周、B君はちょうど4周して同時に地点Pを通過しました。 この間、A君は毎分200mの速さで走りました。 B君は、初めの30秒間は毎分200mの速さで走りました。 その後、B君は、A君に追いつかれるごとに、 追いつかれてから30秒間だけは毎分200mの速さで走りましたが、 それ以外の時間は一定の速さで走りました。 その一定の速さは、最も速くて毎分□m、最も遅くて毎分□mです。 題意が分かればそんなに難しくないと思います 自分でやってみましょう はやとちりすると、2問とも間違ってしまうある意味こわい問題 1000÷8=125 900÷7.5=120 答え 順に 125 120 |
灘中学 入試問題 2016年度 ( 平成28年度 )入試 算数1日目 5番 オイラーの関数 素数 互いに素 1000以下の整数のうち、2でも3でも5でも割り切れない整数を 小さいものから順に並べると 1,7,11,13,17,・・・・・・・,997 となります。 このなかで、一の位の数が7である整数は全部で□個あります。 また、7で割り切れる整数は全部で□個あります。 素数の楽しさを味わえる問題です 問題文の中に10以下の素数2,3,5,7が全て出てきています 2,3,5の最小公倍数は30ですから、1から30までの整数のなかで 2でも3でも5でも割り切れない整数を 書き出していきます でもここで、問題文のなかに 1,7,11,13,17というように17までは書いてくれています ここで灘の算数の問題は分かる人だけに分かるヒントが 問題文の中や例の中に隠されています 別に1,7,11,13,・・・・・・・,997というふうに問題分を書いても、 1,7,11,・・・・・・・,997と書いてもいいと思いませんか? それなのにどうして1,7,11,13,17というように17まで 書いてあるのでしょう? そのあと全部2,3,5で割り切れないことをチェックしていってもいいのですが、 13+17=30が使えることを知っている人だけに ちょっとでも有利になるように17まで書いてくれていると思います。 そこまで算数を楽しんでいる人を 灘が求めているのではないでしょうか? ここで灘中に上位合格する人たちが知っていることを 書いておきます ワンポイントアドバイス 13+17で30ですね あとは30−11で19 30−7で23 30−1で29となります(説明略) だからいっきに 1,7,11,13,17,19,23,29と書き出せます あとは30ごとに繰り返します  30までに一の位が7であるのは2つあります 1000÷30=33・・・10 2×33+1=67 灘中に上位合格する人たちは上の数表すべて書き出していません 前半の問題を解くのに 実際の試験上で計算用紙に書き出しているのは 最初の一行(1,7,11,13,17,19,23,29)で十分です 30ずつ繰り返すので、書かなくていいことが頭のなかでわかっています 30ずつ繰り返すことを意味も分からず、ただ覚えるのではなく、 理由を考えてみましょう。そうすると、 最初の一行で十分であることが理解できますね 最小公倍数のすごさ、素数のすごさ、繰り返すことのすごさを 感じられるのではないでしょうか つぎに後半の解き方ですが 30と7の最小公倍数は210ですので、 210までのなかで7で割り切れる整数をみつけます 上の表の赤枠の中で7の倍数は何個ありますか? これから受験の方は時間を計ってやってみましょう この作業がわりと時間がかかりますし、 計算ミスの可能性もありますね。 100までの7の倍数は普段練習しているので すぐに判定できると思います 100超えてからの7の倍数判定が時間がかかると思います 赤枠の中の4行目91を見つけてほっとしませんでしたか? これは一行に一つ7の倍数があるからあとは簡単と思ったら落とし穴に はまってしまいます 119も7の倍数ですよ  119が7の倍数であることを見つけても 121から209までの24個の整数全部を7で割るのはしんどいですよね? ここで違う思考回路を紹介します 使っている方も多いと思いますが 119が7の倍数とわかったら、そのことを活用するのです 7の倍数に7を足しても7の倍数ですね 頭のなかで126は表にないな 次は133これは表にある 140,147,154・・・・・・・という感じでやる方法です 時間がたっぷりあるときはもちろんどんな方法でもいいです これで赤枠の中に7の倍数が8個あることがわかりました 1000÷210=4・・・160 赤枠の中で160までの7の倍数は6個だから 8×4+6=38 これで答えは出ましたが、何か気づきませんでしたか? 赤枠をよ〜く見てください 今度は縦に数字を見ていってください どの列にも7の倍数が1つずつありますね これは偶然ではないんですよ 理由がわかったらおそらく感動するかも 縦に見ていくということは30ずつ足していってますね 30を足すということは 30÷7=4・・・2 7で割った余りが2ですから 縦に2を加えていくと7で割った余りになります ということは、赤枠の中全部を7で割る必要がなくなります 最初の一行目(1,7,11,13,17,19,23,29)の整数を 7で割って余りを書き、縦に2を加えていく方法で 0になるところが、7の倍数です  この方法だと大きな数を7で割るという作業をしていませんね だから後半の問題を速く正確に解けますね 問題を解くこととは関係ありませんが 表をよく眺めていると 赤枠の中のど真ん中を点対称の中心として 対応するところを足すと7で割り切れるようになっています  もう一度上の表を見ると、  これってすごくないですか? 数の性質って美しいですね ここまで読んでくれたあなたに 最後に後半の問題を表を書き出さずに、 最初の一行(1,7,11,13,17,19,23,29)だけで解く方法を 紹介しておきます この8つの数をそれぞれ7倍してみてください そして、先程の上の表を見てください 先程がんばって探した7の倍数すべて (赤枠の中の青丸で囲んだ数)が 最初の一行(1,7,11,13,17,19,23,29)の7倍に なっていませんか? あまりの美しさに見惚れてしまいます ということは、本当に深く理解していたら、 最小公倍数210までに7の倍数が8個あることと 1000÷210=4・・・160 160÷7=22・・・6 最初の一行をみて、22までだから 1,7,11,13,17,19の6個 8×4+6=38 楽しんでいただけましたでしょうか 答え 順に 67 38 |
灘中学 入試問題 2016年度 ( 平成28年度 )入試 算数1日目 6番 大きな整数のかけ算 7777777777×7777777777を計算すると20桁の整数になります。 この20桁の整数の上10桁、下10桁を取り出して、 それぞれ10桁の整数 A, B をつくります。 このとき、A + B = □ です。 ただし、例えば4桁の整数5678の上2桁、下2桁を取り出して、 それぞれ2桁の整数C,Dをつくると、C=56、D=78、C+D=134です。 7が10個あります 1が9個のときの掛け算で 111111111×111111111=12345678987654321 が有名ですので、知っていれば 1が10個のときの掛け算でやればいいので 1111111111×1111111111=1234567900987654321 となって後は49倍すればいいので一工夫すれば解けます いろいろな解き方がありますが、受験生目線で解いてみます 7777777777×7=54444444439だから ずらして10回書く 54444444439は11桁に注意  ここまではいいのですが、普通に筆算の足し算で計算すると 出来なくはないですが、時間がかかりますし、計算ミスが出そうです 問題文をよく読んでどんなことをしているのかをイメージしてください 掛け算をして20桁の整数の上10桁をA、下10桁をBとして A + Bを求めたいのです ここで下10桁のBは上の青い枠を足し算すると 48から始まる11桁の整数になるので、40000000000(11桁) を引いておかなければなりません 上10桁のAは上の緑の枠を足し算して 青い枠の足し算の繰り上がりの4を足しておきます ここまで分かれば後は足し算の工夫です 青い枠と緑の枠の1行目同士を足します 4444444439+5=4444444444(10桁) 2行目も同様に 4444444390+54=4444444444 9行目まではすべて 4444444444になります 10行目は 9000000000+5444444443=14444444443(11桁) 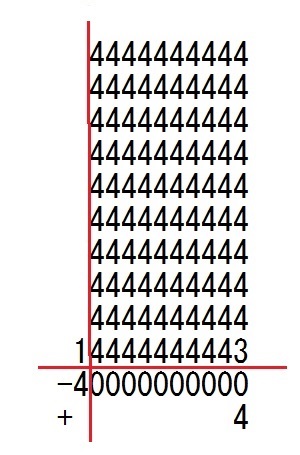 これを計算すればいいのですが、 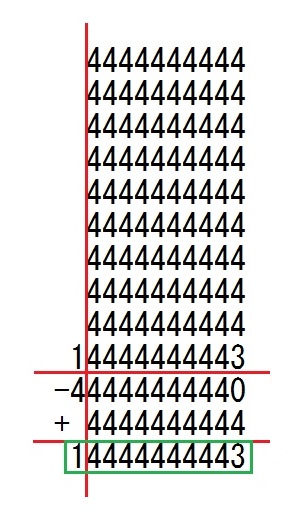 下2行分を −40000000000+4は −44444444440+4444444444と書き換えます この工夫に気づけばもう答えが出ていますね^^; 普段から足し算でも掛け算でも計算の工夫をして来たかどうかが 問われる問題です 他にも解き方がいろいろありますので自分で発見すると楽しいですよ 答え 14444444443 |
灘中学 入試問題 2016年度 ( 平成28年度 )入試 算数1日目 7番 光の反射 解説のみ よく文章を読んで試行錯誤すれば何か気づくでしょう 二等辺三角形です 範囲を求める問題に変わります 普通にやっても実験して本質をつかめばすれば解けます 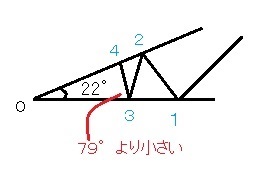 79°より大きかったら、3回めのほうがOに近くなるからダメ 79−22×2=35 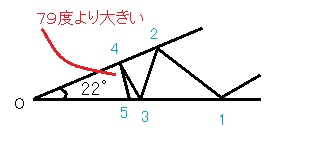 79°より小さかった、5回めのほうがOに近くなるからダメ 79−22×3=13 参考) この手の反射の問題は 甲陽学院中学 1994年 平成6年度1日目 5番 甲陽学院中学 1987年 昭和62年1日目 6番 などに近い問題があります 答え 順に 35 13 |
灘中学 入試問題 2016年度 ( 平成28年度 )入試 算数1日目 8番 正六角形と面積比 右の図のような正六角形 ABCDEF があり、 点 P, Q, R はそれぞれ辺 AB, BC, DEの真ん中の点です。 2本の直線 PR, QF は点 S で交わっています。 このとき、三角形 QRS の面積は、 正六角形 ABCDEF の面積の □ 倍です。 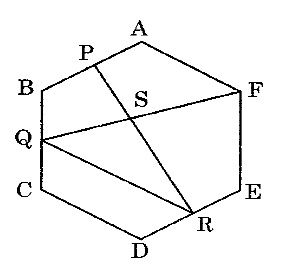 いろいろな解き方があります 中学受験生はどんな解き方でもいいので 答えを合わせないと、、、 方法1 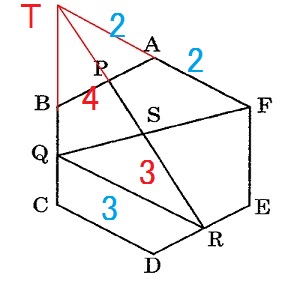 三角形 QRS : 正六角形 ABCDEF = 三角形 QRS : 正三角形 ABT × 6 = 3×3 : 2×7×(2/3)×6 = 9 :56 方法2 四角形 QRFT は台形なので 台形ペケポン面積比を使う 正三角形 ABT = 4 とおくと 三角形 QRS : 正六角形 ABCDEF = 21×(9/49) : 24 = 9 :56 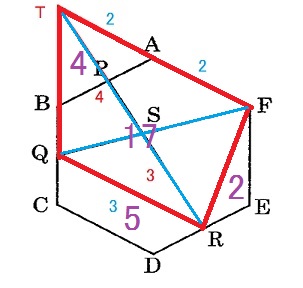 方法3 2辺の積、隣辺比を使う 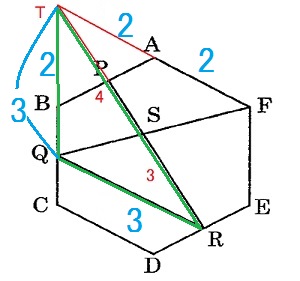 三角形 QRS : 正六角形 ABCDEF = 3×3×(3/7) : 2×2×6 = 9 :56 答え 9/56 |
灘中学 入試問題 2016年度 ( 平成28年度 )入試 算数1日目 9番 図形の移動(直角三角形の転がり) 解説のみ 転がる様子を丁寧に書くだけ π計算を間違わないように工夫する ABC +16π×(1/3) + 4π×(1/4) ー { ABC + 4π×(1/3) + 4π×(1/4)} =(4+3/4)×π =15.70ー0.785 =14.915 参考) 灘中学 入試問題 2010年度 ( 平成22年度 )入試 算数2日目 4番 これが身についていれば出来たでしょう 答え 14.915 |
灘中学 入試問題 2016年度 ( 平成28年度 )入試 算数1日目 10番 平面図形 三角形、四角形の面積 右の図の三角形ABCにおいて、2本の直線ADとBEは点Fで 垂直に交わっています。また (BDの長さ):(DCの長さ)=3:2 (ABの長さ):(CFの長さ)=3:2 です。このとき、FDの長さはAFの長さの□倍で、 四角形FDCEの面積は三角形ABCの面積の□倍です。 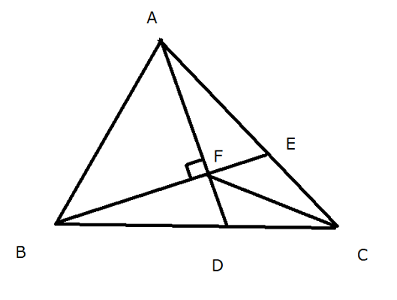 補助線の引き方でいろいろ遊びます 問題文の中に3:2が2つあることから、 何かあやしいなと思うことがまず必要と思います。 後は直角があることから、何を連想するだろうか? ピラミッド相似かちょうちょ相似じゃないかと気づいて、 普段から補助線を引いて試行錯誤することをしていたらうまくいくかも そうじゃないと、与えられた図だけでぼーっと見ていてもしんどいと思います 前半の解き方です 解き方がたくさんありますね あなたのヒラメキを大事にして頭をひねってみましょう 方法1 延長して ピラミッド相似にもっていく 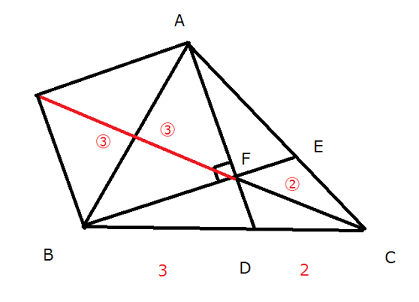 方法2 延長して ピラミッド相似にもっていく 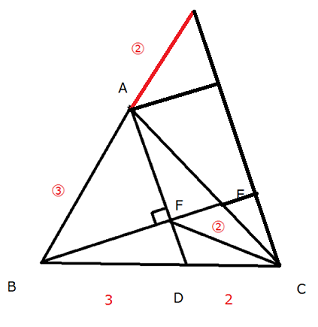 方法3 延長と平行線を引いて ちょうちょ相似にもっていく 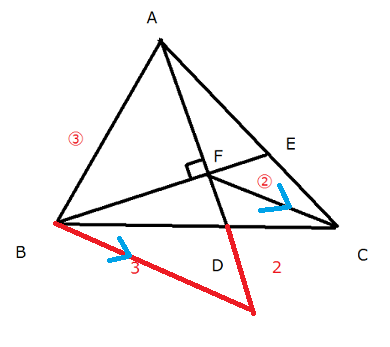 方法4 延長と平行線を引いて さらに垂線を引く ちょうちょ相似と二等辺三角形の性質を組み合わせる 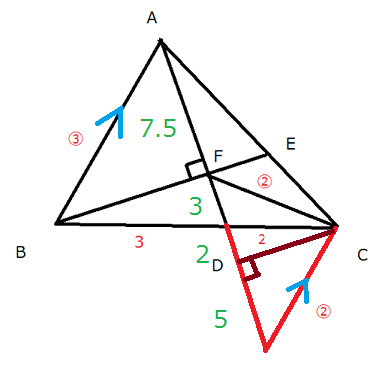 方法5 直角を作って相似に気づく 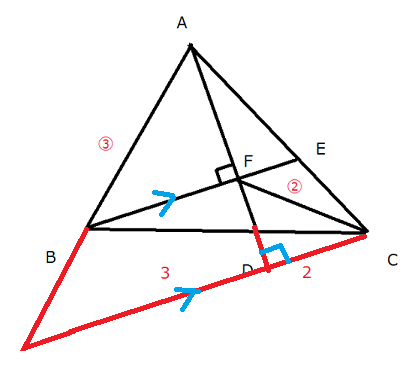 方法6 ほとんど方法5と同じだが直角を作って相似に気づく 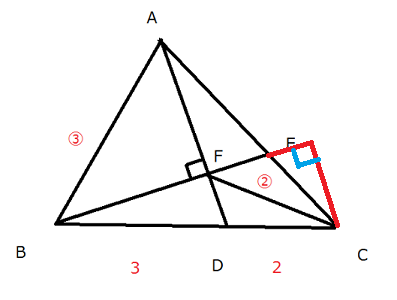 方法7 FCをCのほうにFCの長さの半分の長さだけ延長し、 メネラウスの定理を使う すると1:1の辺の比が出現 後は垂線を下ろしてうまくいきます 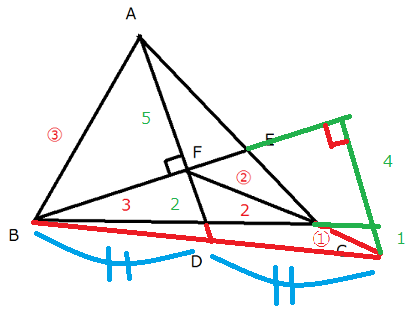 どんな方法でも AF : FD = 5:2であることがわかります 後半はやさしいです AE : EC = 3:2を区切り面積やメネラウスの定理か ベンツ切りなどで求めていけばすぐに求まります 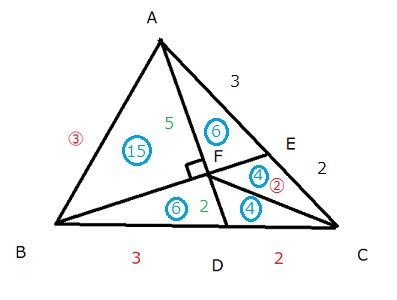 前半が取れた人は後半はサービス問題という感じです 中学受験で合格することを意識すると 前半ができないと後半もおそらく解けないので 2つ分の得点差が開くということになります 答え 順に 2/5 8/35 |
灘中学 入試問題 2016年度 ( 平成28年度 )入試 算数1日目 11番 立体の切断 四角すいの体積 立方体 右の図は、1辺の長さが6cmの立方体です。 この立方体を3点A, I, Gを通る平面で切ったとき、 この平面と辺DHは点Jで交わります。 四角すいKーAIGJの体積は□cm3です。 また、3点B, D, Gを通る平面で 四角すいKーAIGJを2つの立体に分けたとき、 点Kを含む立体の体積は□cm3です。 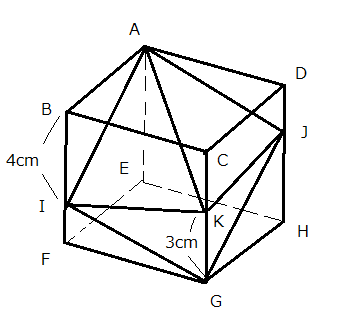 前半の問題は四角すいKーAIGJの体積を求めるのですが 底面を四角形AIGJとみると面積も高さもすぐに出ない このタイプは灘の過去問にもありますが、 立体を平面で分割することです。 それを過去問などで意識してきた方は どう切るかはすぐ浮かぶでしょう 方法1 3点A, K, Gを通る平面で切ってみましょう 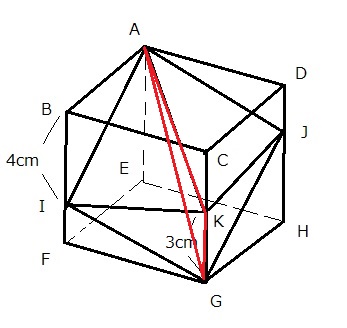 三角すい2つになります そのどちらも体積は18なので 18×2=36 方法2 3点 I, K, Jを通る平面で切ってみましょう 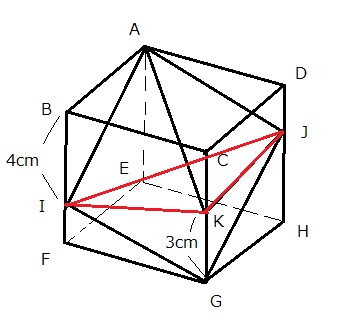 こちらも 三角すい2つになります そのどちらも体積は18なので 18×2=36 理由は少し考えれば分かりますね (ヒント AIGJはどんな四角形ですか?) 後半は 3点B, D, Gを通る平面とAKの交点をMとすると 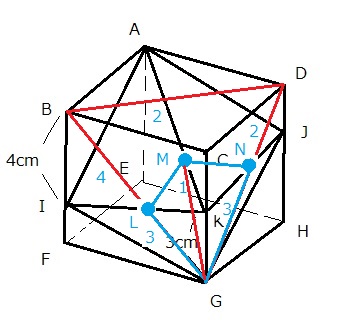 次の図から AM :MK =2 : 1 と分かる 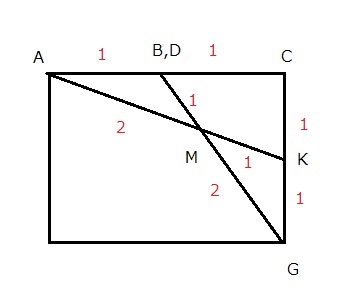 LとNの位置はすぐにわかる 後は四角すいKーMLGNの体積を求めればよい 方法1で前半を求めた方は底面を三角形LGKで、高さは2cmだから 具体的に計算すればよい 少し計算しんどい 工夫してみよう ここでは比をうまく使う方法を紹介しよう 三角すいとAーIGKと三角すいMーLGKを比較して 三角すいとAーIGKは18とわかっているから 三角すいMーLGKは 18×(3/7)×(1/3) 三角すいMーNGKも同様に 18×(3/5)×(1/3)となる 合わせて 18×(1/7+1/5)=216/35 余裕がある人にもう一つ別の解き方を 2014年の灘 算数1日目10番を工夫して解けた方は この問題も同じ手法が使えます 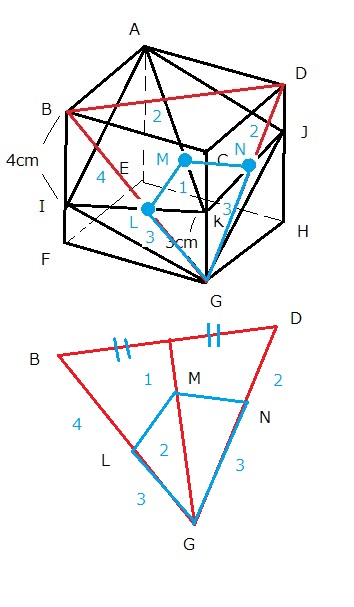 今度は三角すいC-BDGと四角すいKーMLGNを くらべてみよう BGD : MLGN =35 : 12 底面への高さの比が2 : 1 求める四角すいKーMLGNの体積は 6×6×6×(1/6)×(12/35)×(1/2)=216/35 違う解き方を研究すると算数がもっと楽しくなりますね 答え 順に 36 216/35 |
2016年 ( 平成28年度 ) 2016=25×3 2×7 =2×2×2×2×2×3×3×7 =63×32 =211−2 5 =1+2+3+4+5+・・・・・+62+63 (1から63までの連続整数の和) (63番目の三角数) 2016の約数は36個あります 1 2 3 4 6 7 8 9 12 14 16 18 21 24 28 32 36 42 48 56 63 72 84 96 112 126 144 168 224 252 288 336 504 672 1008 2016 2の倍数や3の倍数や7の倍数 平成28年度 28=2×2×7 2016÷28=72 |
2016年に関するやっておきたい中学入試予想問題 ・2016が分母や分子に入った計算問題 (2や3や7で約分できることに注意) ・2016を素因数分解しなさい ・2016の約数はいくつありますか ・2016の奇数の約数はいくつありますか ・2016の偶数の約数はいくつありますか ・2016の約数をすべて書きなさい ・2016の約数の総和はいくつになりますか ・2016の奇数の約数の総和はいくつになりますか ・2016の偶数の約数の総和はいくつになりますか ・2016の約数の逆数の総和はいくつになりますか ・2016を2個以上の連続整数の和で表す方法は何通りありますか ・1/2016から2015/2016までの2015個の分数のうち既約分数の個数 ・1/2016から2015/2016までの2015個の分数のうち既約分数の総和 ・0,1,2,6を使った数列 0,1,2,6の数字だけを使ってできる整数を小さい順に並べた数の列 1,2,6,10,11,12,16,20,21,22,26,60,・・・・・・があります。 (1)2016は何番目にありますか。 (2)2016番目の数は何ですか。 |
灘中学 入試問題 2015年度 ( 平成27年度 )入試 算数1日目 10番 平面図形 60度 三角形の面積 長さ  この問題は答えが合ったから、何も研究せずに、 次の問題に進むよというにはもったいない すごく良い問題だと思います 灘中上位合格目指す人や算数オリンピック決勝に進みたい人などは、 是非この1問でたくさん何かをつかんでください。 答えだけ出すのはすぐ出るかもしれませんが、 解き方がたくさんあり、めちゃくちゃ補助線を引く練習になります この1問でたくさんの公式、技、補助線などが学べます。 たくさん学ばないともったいない。損しますよ 問題集のたくさん問題の解き方を意味も分からず覚えるより、 良問を1問深く学ぶ方が数倍力がつくと思います。 何より算数をもっともっと好きになるでしょうね! 図形に感動するかもしれないし、 上手く補助線が引けて自分のひらめきに感動したりしますよ。 ハマる体験をすると、時間がたつのを忘れるくらい、 没頭する体験が出来るかもしれません(笑) 算数の好きな生徒さんとこの1問を一緒にじっくり考えさせながら、 解き方をすぐに教えるのではなく、 楽しみながら授業をすると3時間あっても足りないと思います 塾で教えてくれる模範解答を覚えるだけより、 算数を通して大事な何かを感じ取れるといいですね。 1問をいろいろな解き方で解くメリットはいっぱいあると思います。 いろんな公式や考え方、工夫などが深まる。 公式などの当てはめ方、使い方がうまくなる。 発想が豊かになる。 なにより、いろいろな解き方を通して、 色々な考え方などが深いところで一つにつながってくる。 頭の中で、言葉で表現できない、 自分の世界観みたいな感覚ができてきます この感覚が得られると、とても気持ちいいですよ。 この3cmと5cmと間の角が120度の三角形は、 BDの長さが7cmとなり七五三(しちごさん)三角形と呼ばれています 大学入試のセンター試験にも出てくる図形です 一工夫する方法は 平行線を引く 垂線を引く 延長線を引く 点と点を結ぶ 回転する 裏返す 二等辺三角形を作る 一部を切って、貼りつける 解き方は10個以上出てくると思います 平行線だけでも、どこに平行線を引くかで3個くらいはすぐに見つかります 回転もどちらに回転させるか、またどの図形を回転させるかでも いろいろ見つかります。 垂線もどの点から引くかでいろいろ見つかります 学べる公式や分野としては、隣辺比、面積比と線分比、相似 正三角形、二等辺三角形、30度問題、角の二等分線, 面積比と相似比、面積比と線分比 など大事なものばかりですね 授業で解説を聞いて理解できるのと、 自分で補助線を引けて答えまで導けるのとでは大きく違います 自分で解けるようになりたい人は、授業を聞くことも大事ですが、 自分ひとりで考える時間も作ってください。 熱中する体験ができれば、学びがどんどん加速していくと思います。 最近の灘中の過去問にも、よく似たテーマが出まくっています。 でも、どの問題も、与えられた図と長さや角度の情報だけでは、 解けないようにできており、 一工夫して自分の持っている知識に結びつける必要があるから、 補助線を引くときに、どうしてその補助線を引くのか? 引くメリットは何かを深めていかないと、 いざ試験の時にはすぐに使えるようにはなりませんよ 答え 順に 6.125 30.625 参考) 灘中学 入試問題 2013年度 ( 平成25年度 )入試 算数1日目 11番 平行線を自分で引くことができれば、解決できます 参考) 灘中学 入試問題 2012年度 ( 平成24年度 )入試 算数1日目 9番 延長線を自分で図に引くことができれば、解決できます 参考) 灘中学 入試問題 2011年度 ( 平成23年度 )入試 算数1日目 11番 点と点を結んで、平行に気づけば、解決できます |
灘中学 入試問題 2015年度 ( 平成27年度 )入試 算数1日目 11番 展開図 立体の体積 三角すいの体積  展開図を組み立てて六角形の面に垂直な平面で 真二つに切って考える 1辺の長さが4cmの正三角形を底面とし、 高さが4cmである三角すいの体積を 1とした時、 組み立てられた立体の体積は (1+2+2)×2=10 別解 高さ平均の公式を使う 1/3 : ((1+2+2)/3)×2=1:10 答え 10 参考) 灘中学 入試問題 2004年度 ( 平成16年度 )入試 算数1日目 11番 これを深く理解していれば、2015年の11番は解ききれると思います 参考)洛南高校附属中学 入試問題 2015年度 算数 8番 (1)(2)(3)(4) これも立方体の1/6倍や1/3倍を使うとすぐ解けます (1) 3×3×3×(1/6)×2=9 (2)3×3×3×(1/6)×(2+2)=18 (3) 3×3×3×(1/3)×(1+2+1)=36 (4) 3×3×3×(1/3)×2×2×2=72 |
灘中学 入試問題 2015年度 ( 平成27年度 )入試 算数2日目 5番 立体の切断 解説のみ (1) 1/36+4/36=5/36 (2)16/36ー3/36=13/36 (3) pを通る平面で切った時 切り落とされる立体の体積は 1/6+8/6=9/6 Rを通る平面で切った時 切り落とされる立体の体積は 125/6ー(6−1/6)=90/6 切り落とされる立体の体積の差を考えると、 90/6ー9/6=81/6=27/2=13.5 別解1 pを通る平面とRを通る平面の間の体積を求め、 実際にはない立体の体積を引く方法 (125/6ー27/6)ー(2×1.5ー1/6)=81/6=13.5 別解2 元の立体の体積216からどれだけ切り落とされているかを比べると、 pを通る平面で切った時 6+1/6+8/6=45/6 Rを通る平面で切った時 125/6+1/6=126/6 126/6ー45/6=81/6=13.5 答え (1) 5/36 (2) 13/36 (3) 13.5 何と何を比べるかを考えると、いろいろな方法で楽しめます |
2015年 ( 平成27年度 ) 2015=5×13×31 13の倍数や31の倍数 平成27年度 27=3×3×3 |
灘中学 入試問題 2013年度 ( 平成25年度 )入試 算数1日目 1番 計算問題 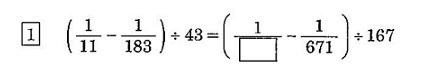 2013=3×11×61 183=3×61 671=11×61 答え 3 2009年の1番と見比べると、おもしろいです 灘中学入試問題 2009年(平成21年)算数1日目1番
|
灘中学 入試問題 2011年度 ( 平成23年度 )入試 算数1日目 2番 11の倍数である5桁の整数で、 各位の数字がどの2つも異なっているもののうち、 最も大きいものは □ です。 答え 98736 |
灘中学 入試問題 2011年度 ( 平成23年度 )入試 算数1日目 3番 2つの商品甲、乙があり、利益はそれぞれ原価の12%、22%で、 甲、乙ともに、原価も利益も1円未満の端数はありません。 また、甲を1つ売ったときと乙を1つ売ったときの利益は同じです。 甲の原価として考えられる金額のうち、最も安いのは □ 円です。 答え 275 |
灘中学 入試問題 2010年度 ( 平成22年度 )入試 算数1日目 4番 3600本の鉛筆を同じ本数のいくつかの束に分けます。 □ 本ずつの束に分けた場合と比べると、 1束の鉛筆を3本ずつ減らした場合の方が、束の数は60だけ増えます。 答え 15 |
灘中学 入試問題 2010年度 ( 平成22年度 )入試 算数1日目 2番 N君の家は0.5ヘクタールの田んぼを所有し、いねを育てています。 その家の田んぼでは、1年間で10アールにつき0.5トンの米がとれ、 N君の家はその米を10kgあたり4000円で売っています。 利益はそのうち12%であるとすると、N君の家が、 とれた米をすべて売ることで1年間に得る利益は □ 万円です。 答え 12 |
灘中学 入試問題 2010年度 ( 平成22年度 )入試 算数1日目 5番 6けたの整数ABCDEFで、 一番上の位の数字Aを一番下の位に移した数BCDEFAが もとの数の3倍になるものは、ちょうど2つあります。 このような数ABCDEFのうち大きい方をXとすると、X=□ です。 また、 X / 999999 をできる限り約分した分数は □ です。 答え 順に 285714 2/7 |
灘中学 入試問題 2010年度 ( 平成22年度 )入試 算数1日目 8番 11で割ると小数第2位が3になり、 13で割ると小数第1位が6になる整数を考えます。 このうち最も小さいものは □ で、 2番目に小さいものとの差は □ です。 答え 順に 73 66 |
灘中学入試問題 2008年(平成20年)算数1日目2番
灘中学入試問題 2008年(平成20年)算数1日目3番
灘中学入試問題 2007年(平成19年)算数1日目3番
灘中学入試問題 2007年(平成19年)算数1日目4番
灘中学入試問題 2007年(平成19年)算数1日目7番
灘中学入試問題 2006年(平成18年)算数1日目2番
おもしろ算数問題 2022年(中学入試)にチャレンジはコチラ →おもしろ算数問題 2022年(中学入試)
おもしろ算数問題 50問(中学入試)にチャレンジはコチラ →おもしろ算数問題 50問(中学入試)
灘中学算数入試問題解説はコチラ → 灘中学算数入試問題
2017( 素数 )年中学入試予想問題はコチラ →2017年中学入試予想問題
おもしろ算数問題 2016年(中学入試)にチャレンジはコチラ →おもしろ算数問題 2016年(中学入試)
おもしろ算数問題 2015年(中学入試)にチャレンジはコチラ →おもしろ算数問題 2015年(中学入試)
2022年中学入試予想問題はコチラ →2022年中学入試予想問題
おもしろ算数問題 2022年(中学入試)にチャレンジはコチラ →おもしろ算数問題 2022年(中学入試)
2022=337×2×3 337は素数です 337は素数です 奇素数337は2つの平方数の和で表される |
2023年度中学受験予定の方へ 2023=7×17×17 2023は素数ではありません 7や17や119や289などの倍数です 2000から2100までの素数は 2003,2011,2017,2027,2029, 2039,2053,2063,2069,2081, 2083,2087,2089,2099の14個あります
|
■トップページ
■算数・数学スーパー個別指導のご案内
■灘中学算数入試問題
■おもしろ算数問題 50問(中学入試)
■お問い合わせ