■トップページに戻る
■算数・数学スーパー個別指導のご案内に戻る
■中学受験算数を楽しく極めたい(ブログ)
■おもしろ算数問題 50問(中学入試) ■2009年灘中学算数入試問題
この下に続くおもしろ算数問題の中から
あなたのお気に入りの問題がひとつでも見つかるといいですね
自分の頭で考える喜びを味わってみてください
解けた瞬間の感動の喜びをあなたも味わってみて〜〜それでは、ごゆっくりどうぞ
算数1番 図1の四角形ABCDは平行四辺形であり、点E,F,Gは それぞれ辺AB,CD,DA上の点で、 AE=EB、 AG=GD、DF:FC=4:1 です。 また、点HはEFとBGの、点IはEFとCGの交わる点です。 このとき、次の問いに答えなさい。 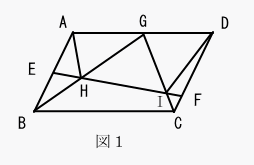 (1) 辺DAを延長した直線と、FEを延長した直線の交わる点をPとします。 また、辺BCを延長した直線と、EFを延長した直線の交わる点をQとします。 このとき、PA:ADとBC:CQを求めなさい。 (2) GH:HBとGI:ICを求めなさい。 (3) 三角形AHGと三角形GHIと三角形GIDの面積の比を求めなさい。 |
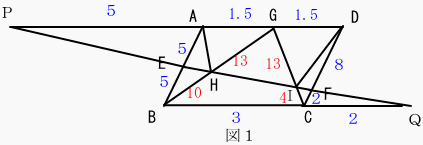 (1) PA:AD=5:3 BC:CQ=3:2 (2) GH:HB=6.5:5 =13:10 GI:IC=6.5:2 =13:4 (3) (三角形AHG):(三角形GHI):(三角形GID) =(13/23):2×(13/23)×(13/17):(13/17) =17:26:23 答 (1) PA:AD=5:3 BC:CQ=3:2 (2) GH:HB=13:10 GI:IC=13:4 (3) (三角形AHG):(三角形GHI):(三角形GID) =17:26:23 |
2009年開成中学入試問題 算数3番 小数問題←←小数問題をもっと楽しもう〜〜
2009年桜蔭中学入試問題 算数1番(1)−3 計算問題←←計算問題をもっと楽しもう〜〜
2009年麻布中学入試問題 算数5番 平面図形 面積比 正六角形
2009年女子学院中学入試問題 算数5番 数の性質 平均
2009年洛南高校附属中学 算数3番
2009年洛南高校附属中学 算数2番(1)分数問題
2009年洛南高校附属中学 算数2番(2)既約分数
2009年洛南高校附属中学 計算問題 算数1番(1)
灘中学入試問題 2009年(平成21年)算数2日目4番
灘中学入試問題 2009年(平成21年)算数1日目6番
灘中学入試問題 2009年(平成21年)算数1日目4番
灘中学入試問題 2009年(平成21年)算数1日目2番
灘中学入試問題 2009年(平成21年)算数1日目1番
おもしろ算数問題 49 ( 灘中 ) にチャレンジ ^^; ←おすすめ
おもしろ算数問題 48 ( 灘中 ) にチャレンジ ^^;
おもしろ算数問題 47 ( 灘中 ) にチャレンジ ^^; ←おすすめ
おもしろ算数問題 46 ( 灘中 ) にチャレンジ ^^;
おもしろ算数問題 36 ( 灘中 ) にチャレンジ ^^;
おもしろ算数問題 29 ( 灘中 ) にチャレンジ ^^;
おもしろ算数問題 28 ( 灘中 ) にチャレンジ ^^;
おもしろ算数問題 27 ( 灘中 ) にチャレンジ ^^;
おもしろ算数問題 20 ( 灘中 ) にチャレンジ ^^; ←おすすめ
■トップページに戻る